Admission CTAs
Mathematics Colloquium: The Parallel Postulate and Geometries without Rigidity
Speaker: Edwin O'Shea, James Madison University
Title: The Parallel Postulate and Geometries without Rigidity
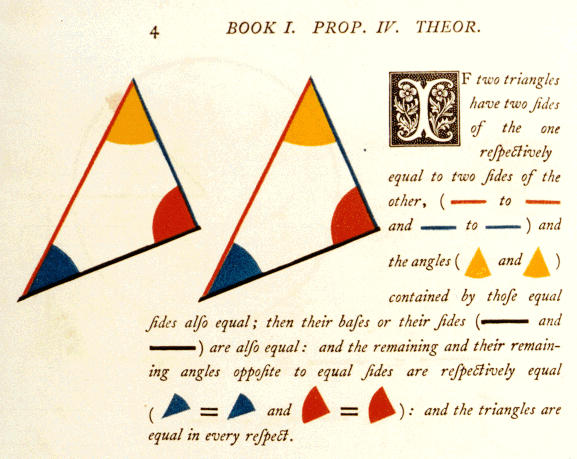
Abstract: The discovery of non-Euclidean geometry in the 19th century elicited two distinct reactions from mathematicians wishing to preserve the ethos of classical geometry: address the crises of foundations (led by David Hilbert and others) and recast geometry vis-a-vis transformation groups (led by Felix Klein and others). This talk aims to build a bridge between these paradigms by exploring axiomatic models of geometry without Hilbertian SAS congruence / Kleinian rigidity. Using these models, we show that the classical equivalence of Euclid’s parallel postulate and Playfair’s axiom collapses in the absence of SAS and that a perfectly standard sum of angles property is equivalent to SAS. The first half or so of this talk will serve as an introduction to Euclid's Elements and its progeny at a level suitable for undergraduates so an in-depth knowledge of the axiomatic development of geometry will not be assumed. This is joint work with my colleague, Elizabeth T. Brown and our four REU students, Emily Castner, Stephen Davis, Edouard Seryozhenkov, and AJ Vargas (J. Geom. (2019) 110: 42), and ongoing work with Brown.
Time: Friday, November 1, 2019, 3:30-4:20 p.m.
Place: Exploratory Hall, room 4106
Refreshments will be served at 3:00 p.m.