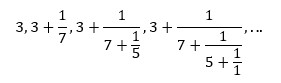Admission CTAs
Mason Mathematics Professor Receives Simon’s Collaboration Grant
The Simon’s Foundation Collaboration Grant for Mathematicians provides researchers in the math community with funding for travel and collaboration, with the goal of stimulating progress on the research of fundamental questions in the mathematical research community. The Simon’s Foundation provides this grant to researchers which they deem capable of tackling those problems which are of great importance, hence it is a distinguished honor to receive this grant. The Department of Mathematical Sciences would like to congratulate Dr. Lukyanenko for his reception of the Simon’s Collaboration Grant for Mathematicians.
Dr. Lukyanenko is an assistant professor of mathematics at George Mason University. His research combines the study of metric geometry with a wide array of other fields including, but not limited to, group theory, dynamical systems, analysis, and number theory.
Dr. Lukyanenko enlarged upon his plans for his use of Simon’s Grant:
“The research funded by the grant focuses on number representations in exotic spaces, including complex numbers, quaternions, octonions and beyond.
Continued fractions approximate numbers by "correcting the denominator" of a fraction.
For example, pi can be approximated, with increasing quality, as seen in Figure 1 below. This, in fact, gives the best approximates of pi.
About 10 years ago, my collaborator Joseph Vandehey and I realized that this approximation method doesn't rely on that many properties of the real numbers, and so can be used more broadly... this led us to formalize the idea of Iwasawa continued fractions, which include all of the examples above, as well as continued fractions in the Heisenberg group, which comes up in applications ranging from complex hyperbolic geometry to quantum physics to parallel parking.
The grant will fund our continued collaboration on this topic, as well as some new directions that I'm exploring with other researchers. It will also fund travel for speakers at the seminar "Geometry: Metrics, Measures, and Algorithms," providing student training and new ideas for research directions.”